I noticed that I had a fairly low amount of posts in the “physics” category, for somebody working in physics & collision detection all day long. So let me try to increase the ratio a bit.
Last time we talked about partial hulls, today I’ll present another optimization for the same problem.
The penetration depth between two convex polytopes can easily be computed using separating-axis tests. But the large number of edge-edge tests often makes this process very slow, and other algorithms such as EPA or Xenocollide are thus often chosen over SAT to compute the MTD between two convexes. There are however a large number of tricks to optimize the SAT version. One of the most efficient ones is to use simple “internal objects”, i.e. simple objects such as a sphere or a box embedded in the convex.
Recall that for each candidate axis we do something like:
bool testSepAxis(const btVector3& axis, const MyConvex& hull0, const MyConvex& hull1, float& dmin, Vector3& mtd)
{
// Project hull 0 on candidate axis
float Min0,Max0;
hull0.Project(axis, Min0, Max0);
// Project hull 1 on candidate axis
float Min1,Max1;
hull1.Project(axis, Min1, Max1);
// If the projected intervals don’t overlap, the candidate axis is a separating axis.
// In that case the hulls don’t overlap, we can early exit and return non penetration.
if(Max0<Min1 || Max1<Min0)
return false;
// Else compute penetration depth (PD) = how much the intervals overlap
const float d0 = Max0 - Min1;
const float d1 = Max1 - Min0;
const float depth = d0<d1 ? d0:d1;
// Then keep track of minimal PD. The axis for which the PD is minimal is the MTD.
if(d<dmin)
{
dmin = d;
mtd = axis;
}
return true;
}
So we’re looking for the minimal overlap, and the MTD is the axis for which the overlap is minimal. The idea, then, is to first project the simpler, internal objects on the candidate axis, and use the overlap results to skip the real hull projections if we can.
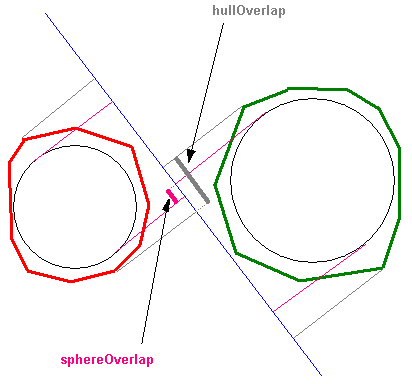
Say our internal objects are spheres (it could also be boxes, but for the sake of the argument let’s use spheres). Let hullOverlap(V) be the overlap value for the hulls on a given axis V, and sphereOverlap(V) be the one for the spheres on the same axis. Since spheres are embedded in the hulls, it should be clear that we always have:
hullOverlap(V) >= sphereOverlap(V) (1) (see Figure 1)
Now let minHullOverlap be our current best result, i.e. our current minimal penetration depth computed from real hull projections (not sphere projections). It should be obvious that thanks to (1) we have:
sphereOverlap(V) > minHullOverlap => hullOverlap(V) > minHullOverlap (2)
In other words, if sphereOverlap(V) is already bigger than our current best result, hullOverlap(V) will be bigger as well, and thus there is no need to compute it.
Figure 1
This is interesting since, of course, projecting a sphere is a lot faster than projecting a convex hull. Projecting a sphere is one dot product, projecting a hull is one dot product per vertex (plus, we don’t need to even access the vertex memory).
As Figure 1 shows, the embedded spheres don’t need to actually touch for this test to be useful - only the spheres’ projections on the candidate axis. In practice, this happens very often, and that single optimization sometimes culls away 90% of the actual hull projections. You can try out
this demo for a proof-of-concept.
It is also a good idea to test the MTD from the previous frame first, to initialize minHullOverlap to a small value right from the start - discarding candidate axes as early as possible.
Finally a note about the internal shapes one should choose. A sphere might not be a great fit for long thin rods, in which case an embedded box might be better. But it might be easier to just use both, and at runtime choose whatever internal shape gives the best results. This is what I do in the above demo.